Why 24 bit audio and anything over 48k is not only worthless, but bad for music.

[danadam]

But don‘t forget the aspect of timing. Humans perceive timing differences in the arrival of wavefronts between left and right ear down to a few microseconds (like 8 to 5 microseconds or even less). That is one aspect of perceiving the direction of a source of sound - you know, in evolution, the famous lion out there that is going to eat you … So, in order to represent such small timing differences in sampled representations of sound, it takes sampling frequencies of more than 100 and up to 200 kHz or more. (More precisely, 1 microsecond corresponds to 1 MHz, 5 microseconds to 200 kHz, 10 microseconds to 100 kHz.)

From https://imgur.com/a/KVFOJU1

A 16 bit, 44.1 kHz file with 33 impulses. Impulses in the right channel (bottom) are exactly 0.5 second apart, while the distance between impulses in the left channel (top) increases by 1.4 microsecond.

The animation skips to each impulse as evidenced by the time bar at the top. The grey waveform is this 16/44 file upsampled 16x. The highlighted area in the middle is 2-samples wide and centers on zero-crossing of the right, "stationary", channel.

(see attachment below for the file with impulses)

 

[71 dB]

Time resolution of 44.1 kHz 16 bit digital audio is at least 1000 times bigger than needed. It is all about how band-limited signals work.

If the time resolution was only 22.7 µs, applying minimum phase filters would be interesting as the phase shift would be quantised to junks corresponding to temporal delays of multiples of 22.7 µs. Fortunately digital audio doesn't work like that.

Digital audio is deceptively easy to misunderstand and surprisingly demanding to understand correctly.

 

[111MilesToGo]

Thanks to all who provided me with all educational stuff, good reads, good links to the theory behind digital audio and video.

And besides, contenance and netiquette are there for a good reason …

 

[71 dB]

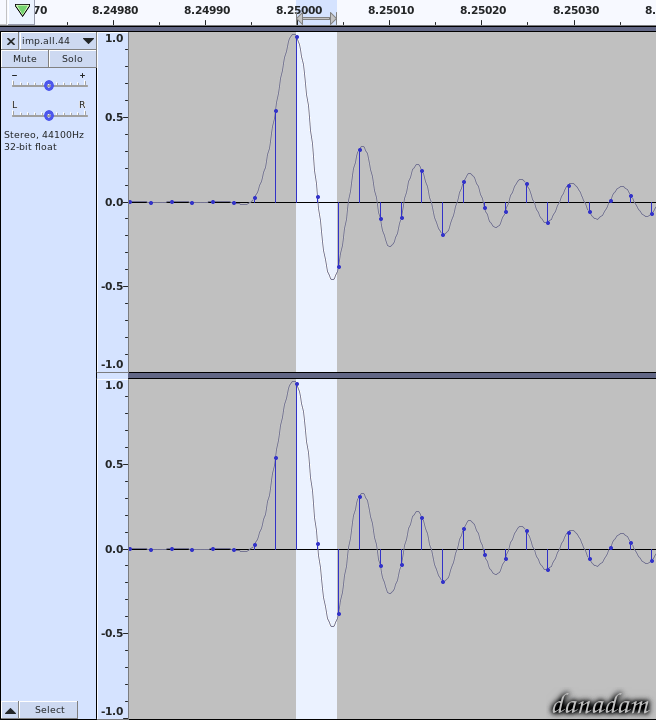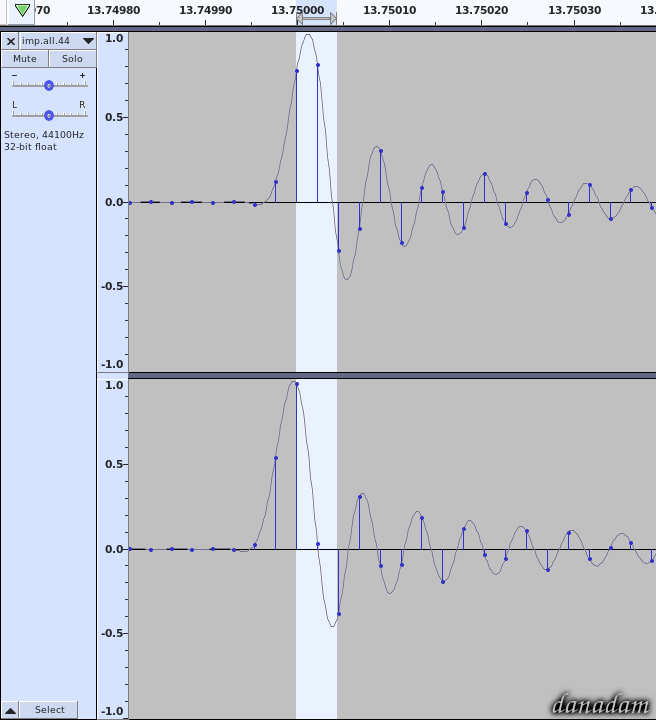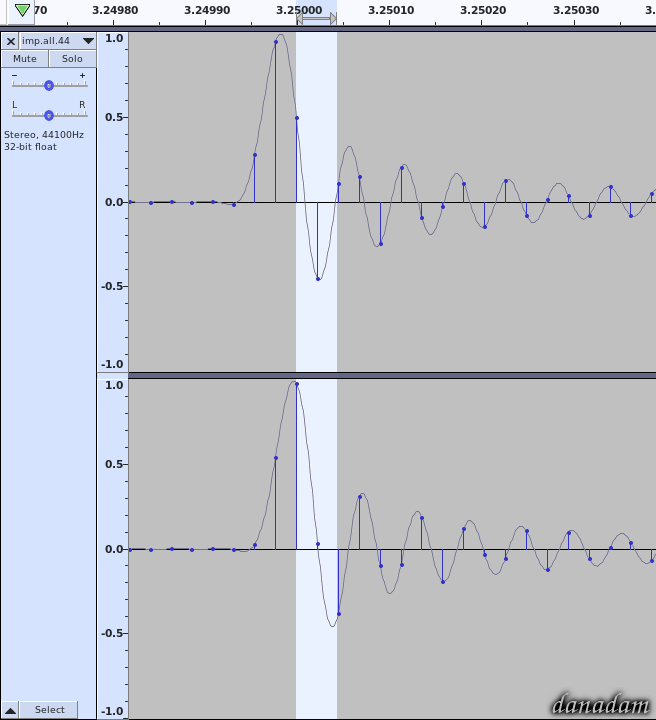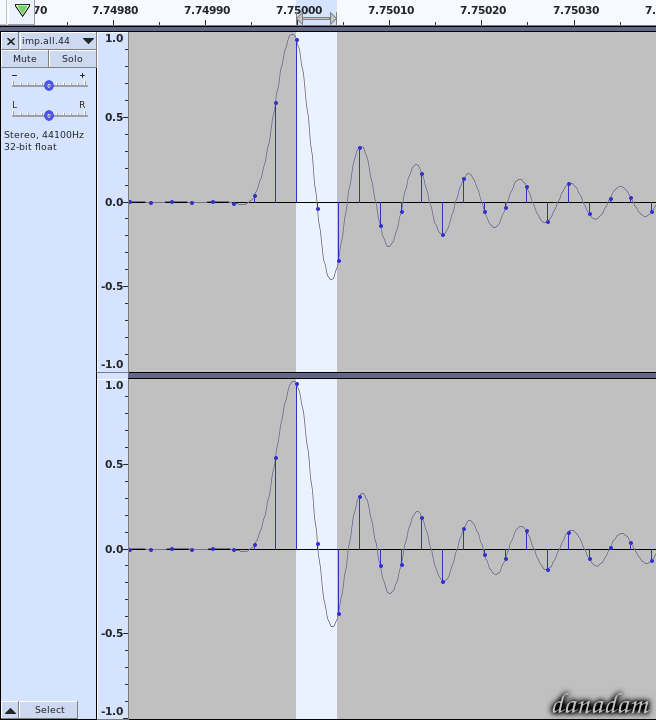
Higher sampling frequencies allow for better representation of the continuous audio waves by the discontinuous sequence of samples (”dots“ on a timeline).

No, they don't if we are talking about band-limited signals and we should be, because sampling theorem requires that signals are bandlimited according to the Nyquist frequency. By bandlimiting the signal, we know 100 % what the signal does between the sample points. There is mathematically only one way it can connect the dots. In order to behave differently the signal would need frequencies above Nyquist, but band-limited signals do not have those!

Also, how audio waves look to our eyes is different from how our ear hear them. For our eye the visual shape of the wave is easy to see, because that's what eyes are for: seeing shapes. Our ears however work differently and are much more into analysing the frequency content of the waveform. Since different looking waveforms can have the exact same frequency content, ears are not interested much about the exact shape of the waveform. In fact, rooms acoustics with all the reflections and reverberation render the original waveform pretty much unrecognisable to the eye, but that doesn't matter much, because for the ear the frequency content is more or less intact (depending on how good the acoustics are). Even speakers/headphones alone change the waveform drastically.

But don‘t forget the aspect of timing. Humans perceive timing differences in the arrival of wavefronts between left and right ear down to a few microseconds (like 8 to 5 microseconds or even less). That is one aspect of perceiving the direction of a source of sound - you know, in evolution, the famous lion out there that is going to eat you … So, in order to represent such small timing differences in sampled representations of sound, it takes sampling frequencies of more than 100 and up to 200 kHz or more. (More precisely, 1 microsecond corresponds to 1 MHz, 5 microseconds to 200 kHz, 10 microseconds to 100 kHz.)

I think that is an easy explanation of what sampling rates are needed for a good representation of sounds by discontinuous samples.

Again, the core idea of the sampling theorem is to represent (band-limited) continuous signals fully by taking samples often enough.

Higher sampling frequency allows sampling of higher frequences. That's all.
Higher bit depth allows lower noise floor. That's all.

For consumer audio 44.1 KHz sampling frequency and 16 bit quantisation allow enough bandwidth (up to 20 kHz) and dynamic range (technically about 96 dB and perceptually up to 120 dB depending on what kind of dithering is used). In music production 24 bit is useful/beneficial for practical reasons and also higher sampling rates may have a place in the production, for example when recording ultrasonic sounds and using them at lower samplerates as sound effects.

 

[71 dB]

Edit: At 44.1 kHz sampling, time discretization errors are of the order 22.7 microseconds (1/44,100 s).

That would be true, I believe, if the bit depth was 1, but it is 16 or more.

 

[MooMilk]

As a delivery format title stays fundamentally true,
For recording - higher sample rates may proof useful for some VST effects (esp. for compression\limiting), and a bit lower latency

 

[gregorio]

For recording - higher sample rates may proof useful for some VST effects (esp. for compression\limiting)

That was true, roughly 20 or more years ago but not today. It’s true that some plug-ins perform better at higher sample rates, certain modelled plugins such as compressors/limiters, certain soft synths and some other plugins, but these days those plugins would over-sample internally, so a higher sample rate file format is unnecessary.

G

 

[Whitigir]

Have anyone even considered about physics beside mathematics? In reality, there are tolerances parameters that play a huge role, and why over sampling. Higher sampling will give better accuracy, because resistors and all other physical components have precision tolerances. For band limited with Nyquist sampling, the tolerances of resistors needed are not existed yet, let alone temperatures drift parameters and so on.

 

[71 dB]

Have anyone even considered about physics beside mathematics? In reality, there are tolerances parameters that play a huge role, and why over sampling. Higher sampling will give better accuracy, because resistors and all other physical components have precision tolerances. For band limited with Nyquist sampling, the tolerances of resistors needed are not existed yet, let alone temperatures drift parameters and so on.

Higher sampling rate can reduce the accuracy when the circuits with their time constants are not "fast enough". That's why this "physics" argument doesn't hold water.

 

[gregorio]

Have anyone even considered about physics beside mathematics?

What physics besides mathematics? There is no “physics besides mathematics” because all physics is defined by mathematics. So of course no one has ever considered physics besides mathematics.

In reality, there are tolerances parameters that play a huge role, and why over sampling.

What do you think those “tolerances parameters” are defined by, if not mathematics? Oversampling is used because it provides the most efficient method of overcoming certain issues. For example the cost/complexity of analogue anti-alias/reconstruction filters or of say emulating ultrasonic freq induced IMD.

Higher sampling will give better accuracy, because resistors and all other physical components have precision tolerances.

Higher sampling does NOT give better accuracy, it gives the same accuracy but over a wider frequency spectrum.

For band limited with Nyquist sampling, the tolerances of resistors needed are not existed yet,

True but you’re contradicting yourself! If the needed tolerances of resistors do not exist yet for 24/48 how will increasing the sample rate “give better accuracy”?

let alone temperatures drift parameters and so on.

A fundamental limitation with resistors is the thermal noise. First measured by Johnson, quantified by Nyquist and published in 1928, this equation defines the amount of thermal noise produced by resistors depending on bandwidth and temperature:

G

 

[Whitigir]

Higher sampling rate can reduce the accuracy when the circuits with their time constants are not "fast enough". That's why this "physics" argument doesn't hold water.

Then why most of the current DAC are all at the least 8X OverSampling ?

 

[gregorio]

Then why most of the current DAC are all at the least 8X OverSampling ?

Because:

Oversampling is used because it provides the most efficient method of overcoming certain issues. For example the cost/complexity of analogue anti-alias/reconstruction filters or of say emulating ultrasonic freq induced IMD.

However, @71 dB is correct, oversampling *can* reduce the accuracy. But the word “can” does not mean “always will”, it depends on how it’s implemented. Just increasing the sample rate, say from 48kFS/s to 192kFS/s, obviously requires processing 4x the amount of data in the same period of time. This can be achieved with no loss of accuracy provided that 4x the processing power is available. There have been implementations which solved the problem by using decimation or reconstruction filters that did not adequately attenuate at the Nyquist point (say 96kHz) and therefore reduced accuracy. Most DACs these days oversample by factors of more than 64x but reduce the processing demand by reducing the bit depth to just a handful.

G

 

[71 dB]

Then why most of the current DAC are all at the least 8X OverSampling ?

Because the benefits of oversampling surpass the negatives.

 

[Whitigir]

Because the benefits of oversampling surpass the negatives.

Thank you! This answers the thread topic itself

 

[71 dB]

Thank you! This answers the thread topic itself

I don't think it answers the thread topic itself, but I'm glad you are pleased.