Recently, I've noticed people in our group chat often miscalculating sensitivity, and I can't find any reliable methods or derivations for sensitivity conversion online (the first few results on Baidu are misleading). So I decided to write this article... BTW, I'm Chinese. Please forgive my poor English since it's not my native language.

The driving difficulty of a pair of headphones, i.e., how "easy or hard it is to drive," can usually be preliminarily judged based on its sensitivity and impedance. Sensitivity is divided into voltage sensitivity (dB/Vrms) and power sensitivity (dB/mW).

Some hifi manufacturers use dB/Vrms, while others use dB/mW (if only dB is written, it's usually dB/mW), which can be confusing. We need to convert both types of sensitivity into the same unit for comparison. For low-impedance headphones, like most planar magnetic headphones, we typically use dB/mW. For high-impedance headphones, such as traditional dynamic headphones, we usually use dB/Vrms. Impedance directly affects the ability of amp to power the headphones. This is a little complex and will be discussed later.

For typical headphones, if any two parameters amone voltage sensitivity, power sensitivity, and impedance are known, the third can be estimated. The following is a rigorous derivation process. If you only want the conclusion, please look at the beginning.
Sensitivity Calculation Formula
Suppose the voltage sensitivity of a pair of headphones is $S_{Vrms}$, the power sensitivity is $S_{mW}$, and the impedance is R. They usually satisfy the following relationship:
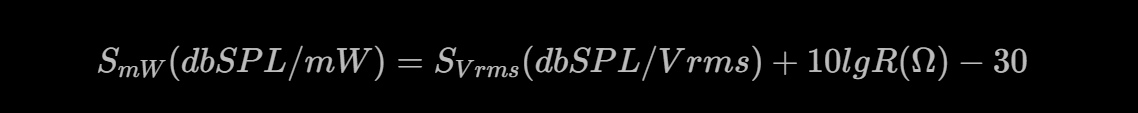
Background Knowledge
Most constant impedance headphones (including dynamic, planar magnetic, and electrostatic headphones) have a direct proportionality between sound pressure (Pa) and equivalent voltage (Vrms), which we call the proportional relationship between sound pressure and equivalent voltage.

Where I is the sound pressure level, measured in decibels (dBSPL, abbreviated as dB); P is the sound pressure, measured in pascals (Pa); P0 is the reference sound pressure, set at 0.00002 Pa; S is the sensitivity, i.e., the loudness of the headphones at 1 Vrms or 1 mW, expressed in dB/Vrms or dB/mW.
Derivation Process


Evaluate Fiio FT5 as a Verification
Let's take the FiiO FT5 as an example (because its official website lists both types of sensitivity and impedance).

According to the official data, the impedance of the FT5 is 32 Ω, and the voltage sensitivity is 110 dB/Vrms. According to our formula, its power sensitivity should be:
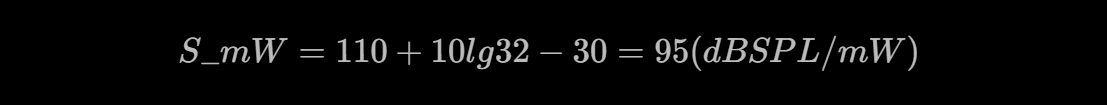
The official mark of FT5's power sensitivity is 96 dB/mW. Considering that decibels are logarithmic units with relatively low precision, our prediction can be considered consistent with the result.
Evaluate Moondrop Cosmo as an Example
Let's use the new flagship over-ear of Moondrop, Cosmo, as an example for a practical demonstration: "How to evaluate the driving difficulty of a planar magnetic headphone


This is part of a promotional image of the Cosmo. It mentions that its sensitivity is 100 dB/Vrms and the impedance is about 15 Ω. For such low-impedance, low-sensitivity headphones, dB/Vrms sensitivity is not an ideal indicator. To judge how hard it is to drive, we need to calculate its dB/mW sensitivity.
The result is: Sensitivity (in dB/mW) = 100 + 10 * lg15 - 30 = 81.8 dB/mW
One of the hardest-to-drive hi-end planar headphones in the world, Susvara, has a nominal sensitivity of 83 dB/mW. The entry-level planar headphone he400se, which audiophiles generally consider hard to drive, has a nominal sensitivity of 91 dB/mW. So obviously, the Cosmo has nothing to do with "high sensitivity, for easy driving" written in its promotional image.
a fun fact:
A Moondrop technician replied to my question about this promotional image: "We'll find out which employee made this and dock his pay." (just a joke, I guess )
)

The driving difficulty of a pair of headphones, i.e., how "easy or hard it is to drive," can usually be preliminarily judged based on its sensitivity and impedance. Sensitivity is divided into voltage sensitivity (dB/Vrms) and power sensitivity (dB/mW).

Some hifi manufacturers use dB/Vrms, while others use dB/mW (if only dB is written, it's usually dB/mW), which can be confusing. We need to convert both types of sensitivity into the same unit for comparison. For low-impedance headphones, like most planar magnetic headphones, we typically use dB/mW. For high-impedance headphones, such as traditional dynamic headphones, we usually use dB/Vrms. Impedance directly affects the ability of amp to power the headphones. This is a little complex and will be discussed later.

For typical headphones, if any two parameters amone voltage sensitivity, power sensitivity, and impedance are known, the third can be estimated. The following is a rigorous derivation process. If you only want the conclusion, please look at the beginning.
Sensitivity Calculation Formula
Suppose the voltage sensitivity of a pair of headphones is $S_{Vrms}$, the power sensitivity is $S_{mW}$, and the impedance is R. They usually satisfy the following relationship:
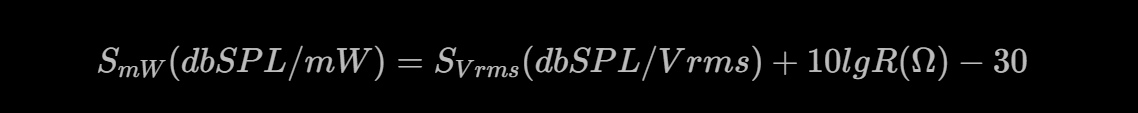
Background Knowledge
Most constant impedance headphones (including dynamic, planar magnetic, and electrostatic headphones) have a direct proportionality between sound pressure (Pa) and equivalent voltage (Vrms), which we call the proportional relationship between sound pressure and equivalent voltage.

Where I is the sound pressure level, measured in decibels (dBSPL, abbreviated as dB); P is the sound pressure, measured in pascals (Pa); P0 is the reference sound pressure, set at 0.00002 Pa; S is the sensitivity, i.e., the loudness of the headphones at 1 Vrms or 1 mW, expressed in dB/Vrms or dB/mW.
Derivation Process


Evaluate Fiio FT5 as a Verification
Let's take the FiiO FT5 as an example (because its official website lists both types of sensitivity and impedance).

According to the official data, the impedance of the FT5 is 32 Ω, and the voltage sensitivity is 110 dB/Vrms. According to our formula, its power sensitivity should be:
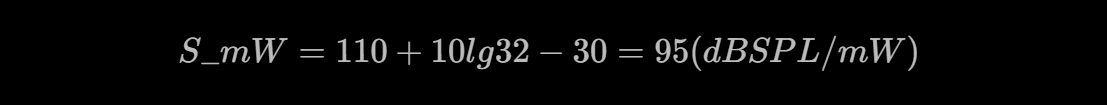
The official mark of FT5's power sensitivity is 96 dB/mW. Considering that decibels are logarithmic units with relatively low precision, our prediction can be considered consistent with the result.
Evaluate Moondrop Cosmo as an Example
Let's use the new flagship over-ear of Moondrop, Cosmo, as an example for a practical demonstration: "How to evaluate the driving difficulty of a planar magnetic headphone


This is part of a promotional image of the Cosmo. It mentions that its sensitivity is 100 dB/Vrms and the impedance is about 15 Ω. For such low-impedance, low-sensitivity headphones, dB/Vrms sensitivity is not an ideal indicator. To judge how hard it is to drive, we need to calculate its dB/mW sensitivity.
The result is: Sensitivity (in dB/mW) = 100 + 10 * lg15 - 30 = 81.8 dB/mW
One of the hardest-to-drive hi-end planar headphones in the world, Susvara, has a nominal sensitivity of 83 dB/mW. The entry-level planar headphone he400se, which audiophiles generally consider hard to drive, has a nominal sensitivity of 91 dB/mW. So obviously, the Cosmo has nothing to do with "high sensitivity, for easy driving" written in its promotional image.
a fun fact:

A Moondrop technician replied to my question about this promotional image: "We'll find out which employee made this and dock his pay." (just a joke, I guess


















































