[atomicbob]

Typical audio device specifications include distortion specifications which are published as follows:

THD less than 0.02%
THD less than 0.02% at 1 KHz
THD less than 0.02%, 20 Hz to 20 KHz, 0 dBu, 300R load

The first specification is meaningless. It provides no information about the measurement conditions. The second is a little better acknowledging THD was measured at a single frequency with no level or load specified. It is not very useful unless you listen primarily to 1 KHz sinusoids. The third specification provides the frequency range over which the measurements were acquired, the voltage level and load used. This is a much more complete and honest specification. Yet greater insight may be derived from viewing the graph which produced that last specification.

Acronyms

THD = Total Harmonic Distortion
THD+N = Total Harmonic Distortion + Noise
dBu = dB referenced to 0.775 Vrms

Consider the following example:

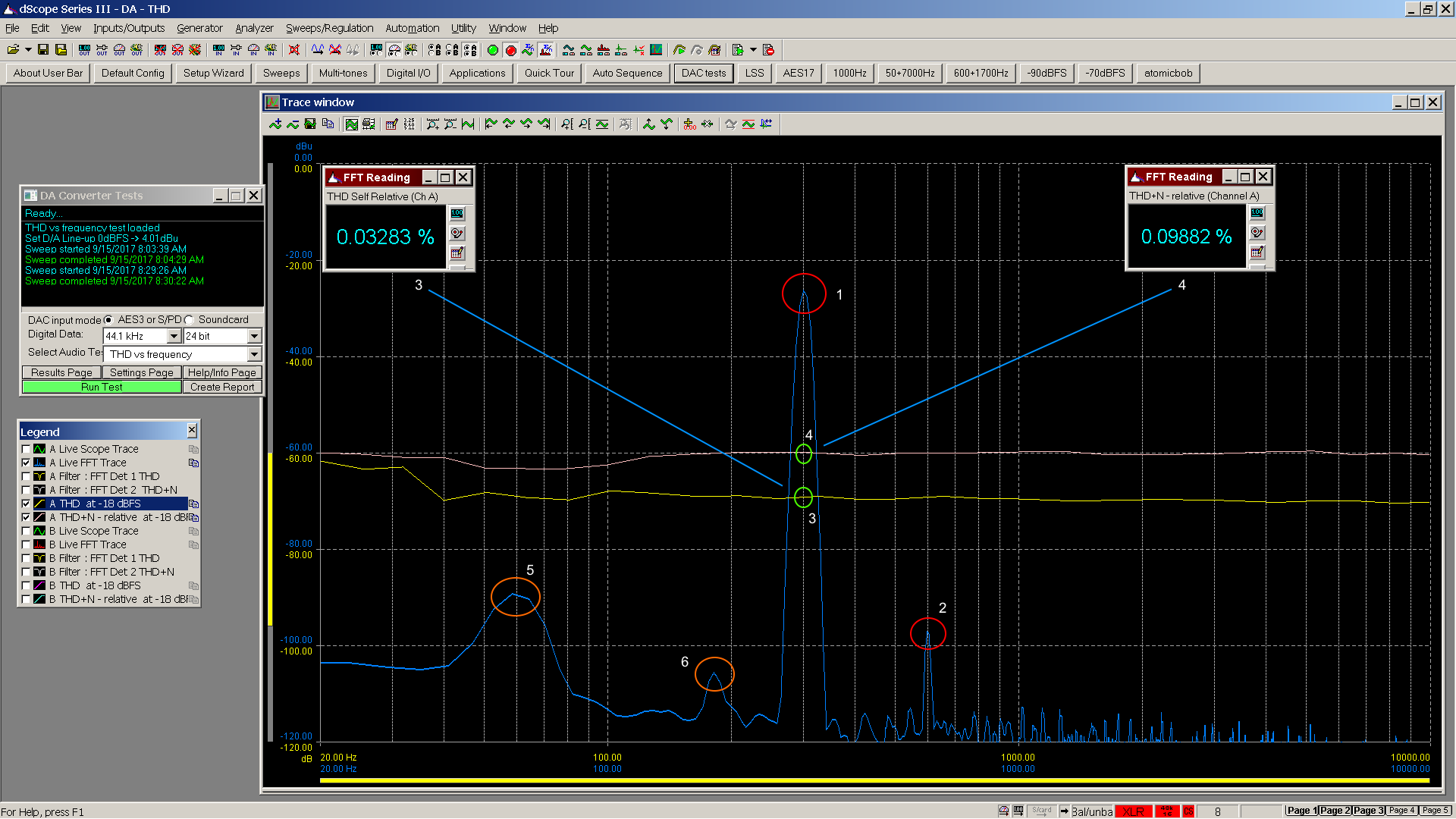
Points of interest

1. Fundamental 300 Hz sinusoid at -26.55 dBu
2. 2nd harmonic 600 Hz sinusoid at -96.22 dBu
3. Calculated THD for 300 Hz both numeric display and point on graph
4. Calculated THD+N for 300 Hz, numeric display and point on graph
5. 60 Hz mains noise at -90 dBu
6. 180 Hz mains noise at -105 dBu

THD adds the dB levels of 2nd and higher harmonics of the fundamental input sinusoid found in the FFT, and compares the result to the fundamental in the FFT.

THD+N adds dB levels of everything in the FFT except the fundamental, and compares to the fundamental, which typically results in a larger number due to inclusion of noise.


Here are some useful equations.

To obtain the graph a sinusoid is swept from 20 Hz to 20 KHz, measuring and plotting the THD and THD+N

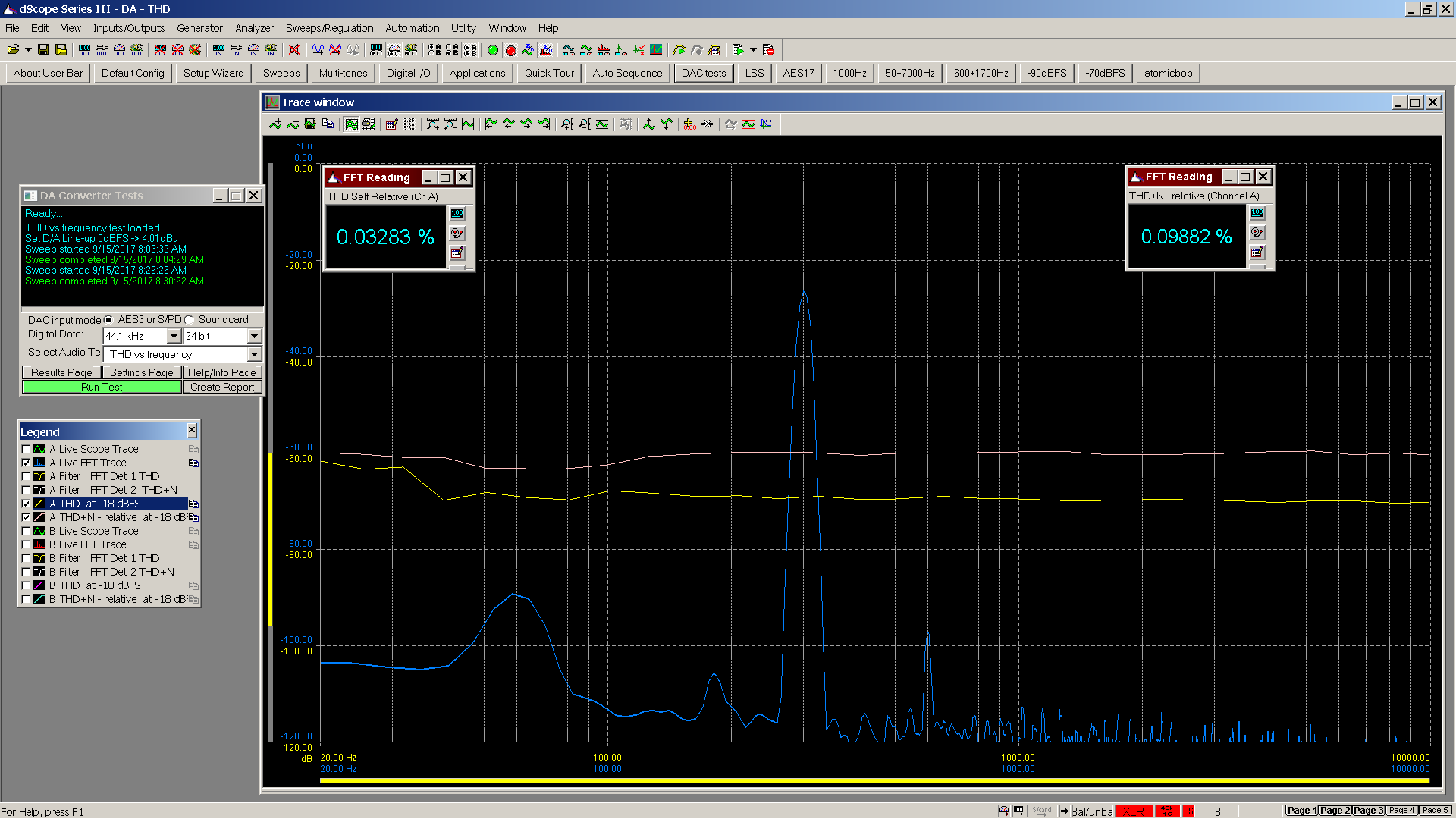
Sample at 300 Hz above. Sample at 1000 Hz below.

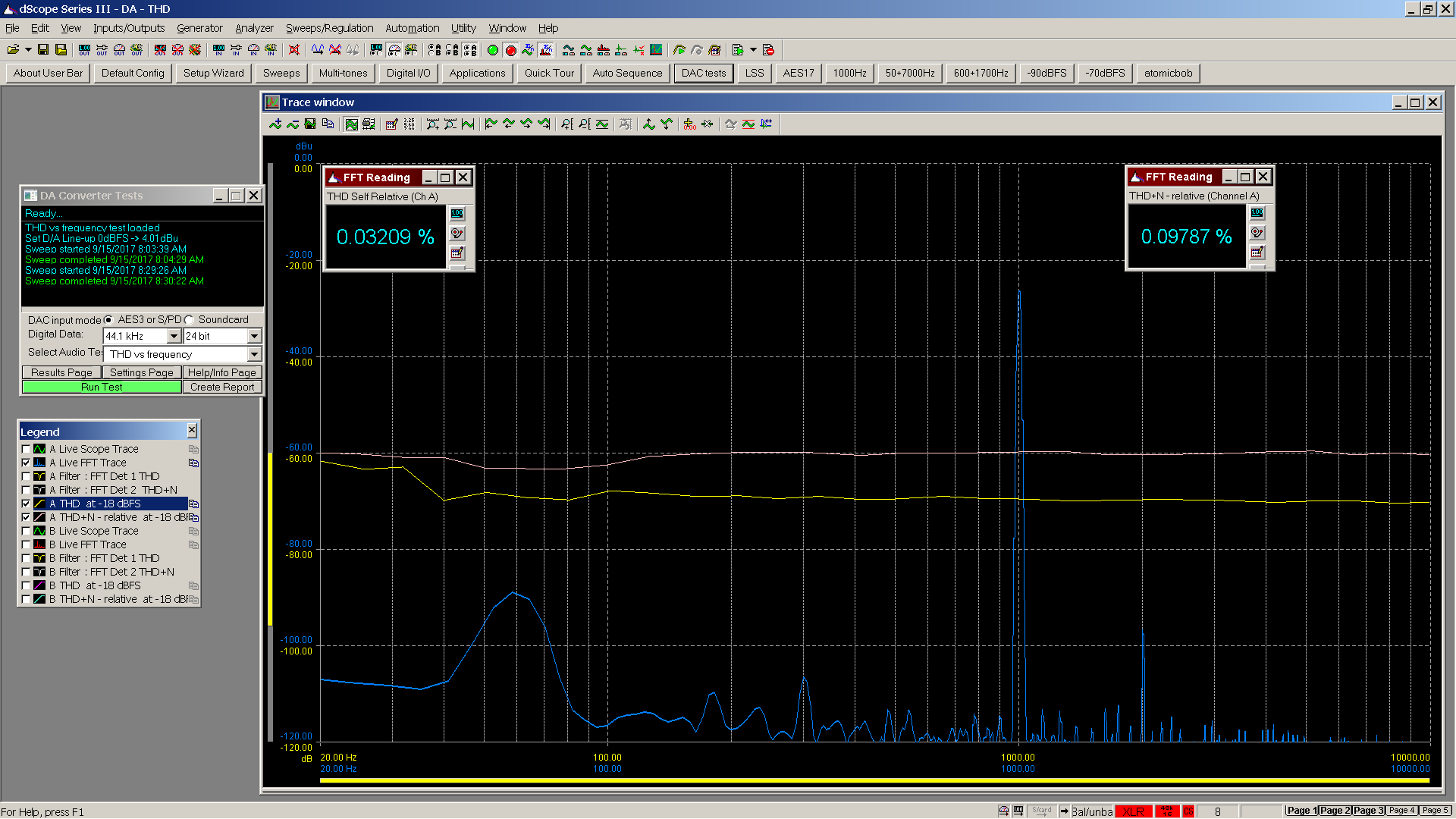
Sample at 3000 Hz.

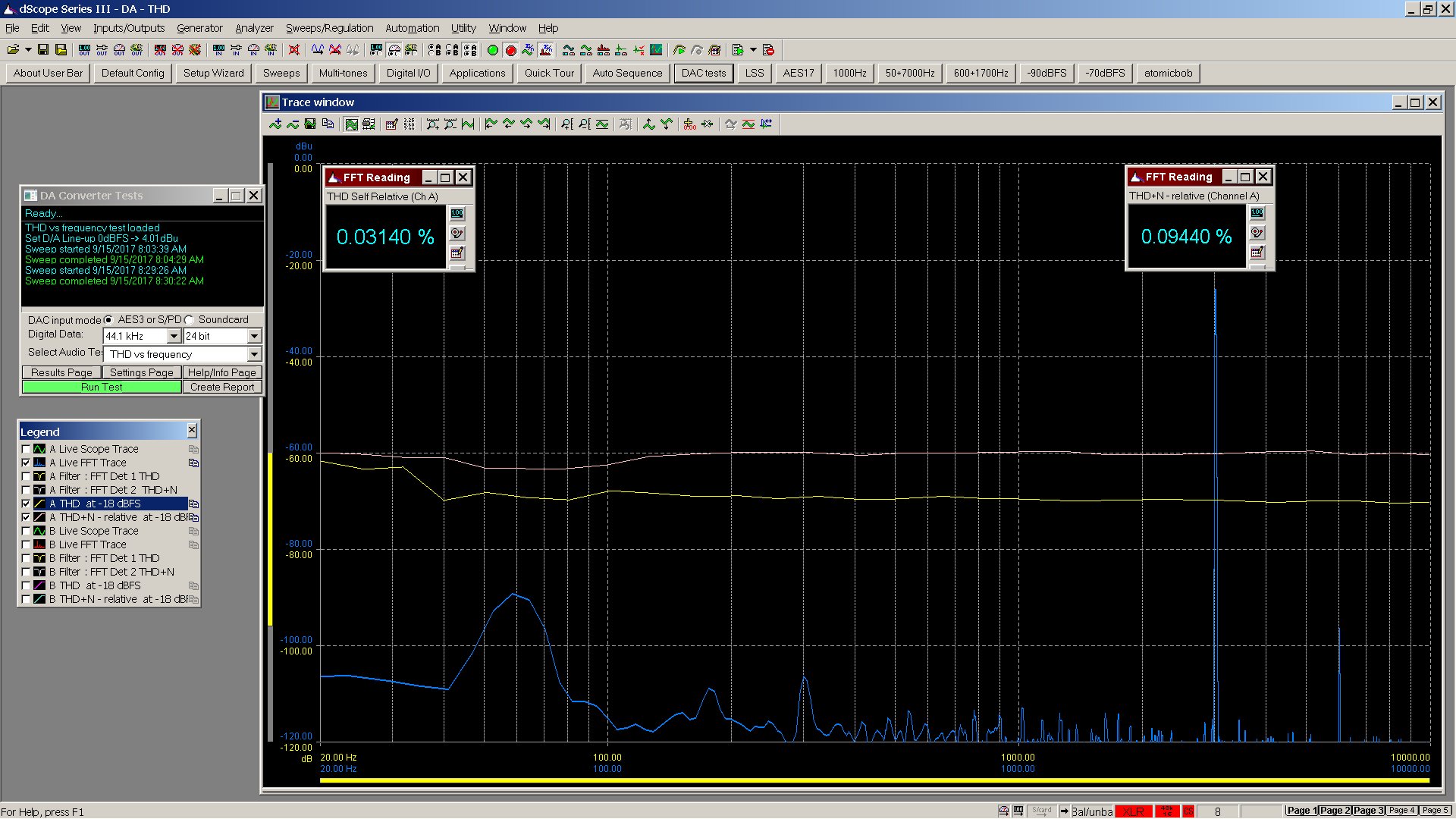
The graph for this device indicates a frequency neutral THD and THD+N. Residual noise observed is low as depicted in the spectrum with the primary residual noise being power supply mains related. However, given -90 dBu translates to 10 dB SPL for an HD800 this should remain inaudible.

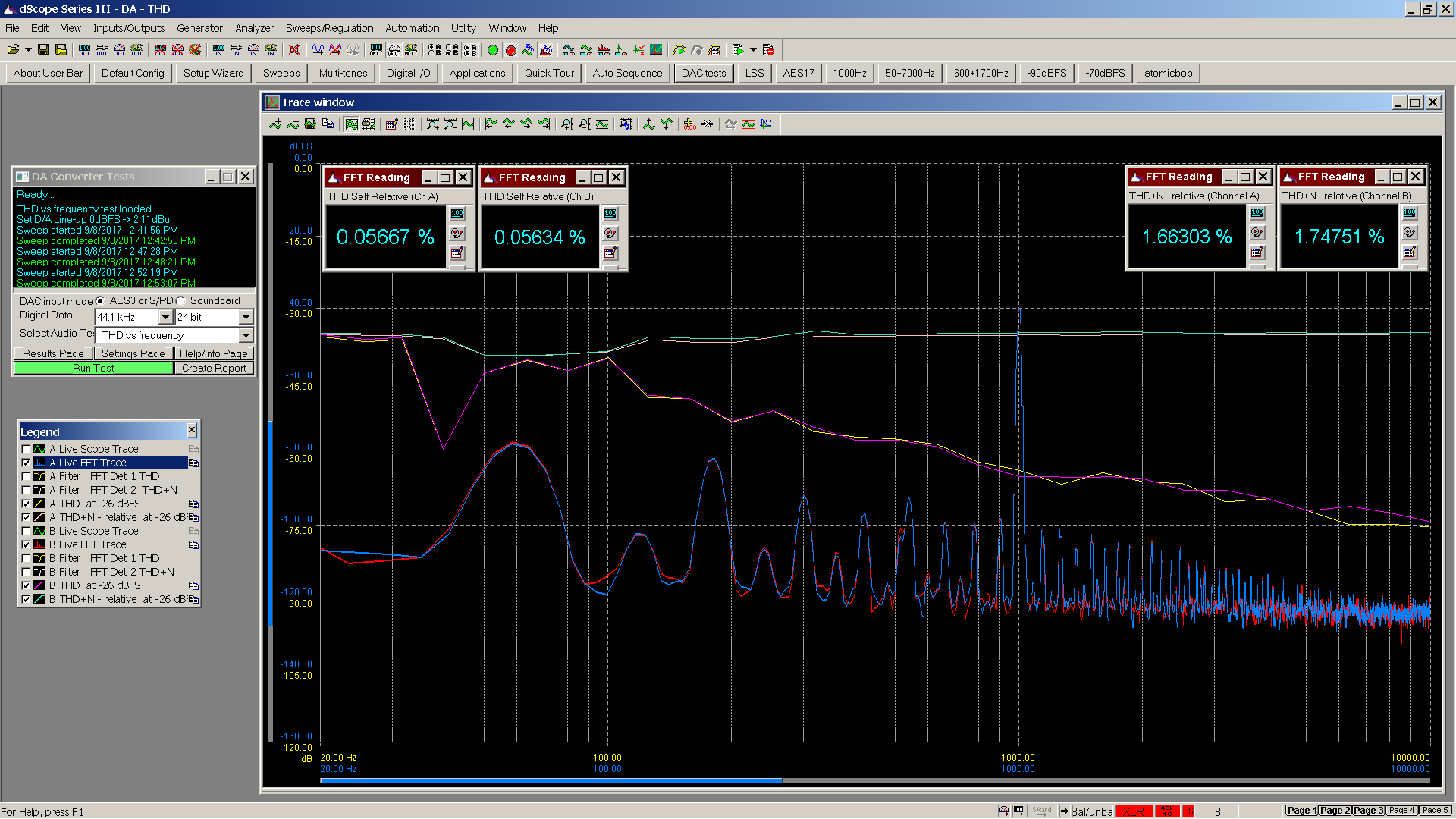
The graph for this device indicates a frequency dependent THD with distortion rising as frequency falls. THD+N is frequency neutral but overall higher than the previous example. Also note the number of spikes in the spectrum. Residual noise (blackground) observed is noisier compared to the previous device measurement. (Please watch the y axis notation – this graph has different scales than the previous examples.)

Further reading:
Fundamentals of Modern Audio Measurements, Richard C. Cabot
http://www.aes.org/e-lib/browse.cfm?elib=7080

 

[Arpiben]

Since we are dealing with FFT based measurements, would you mind sharing typical Audio THD measurement instrument's (dscope) parameters such as:

• Sampling rate
• Bin size
• FFT Window used?

As a side note,even if it is insignificant for low distortion levels ,which THD ratio is computed the one relative to fundamental THD F, or the one compared to the waveform rms value THD R?

I(n) are either the rms values or the amplitudes of the harmonics.
At low values of THD, there is not much difference between the two.
However, the two definitions may cause ambiguity,confusion, and misinterpretation when measuring waveforms of high harmonic content.

 

[atomicbob]

Here is the dScope setup page for THD and THD+N vs frequency:

FFT bin size adapts as the sweep moves from 10 KHz down to 20 Hz. Initially FFT size is 8192 with bin resolution of 5.86 Hz / bin. This is not sufficient resolution for lower frequencies. As the sweep moves downward in frequency, FFT size increases until reaching 65536 for the lower frequencies, which resolves 0.73 Hz / bin.

From the reference cited in the original post above:
Further reading:
Fundamentals of Modern Audio Measurements, Richard C. Cabot
http://www.aes.org/e-lib/browse.cfm?elib=7080

Page 12 under Harmonic Distortion
Total harmonic distortion (THD) is then defined as the ratio of the RMS voltage of the harmonics to that of the fundamental. This may be accomplished by using a spectrum analyzer to obtain the level of each harmonic and performing an RMS summation. This level is then divided by the fundamental level, and cited as the total harmonic distortion (usually expressed in percent).

Also note that wikipedia is attempting to be complete, however the discussion includes power systems which are rather different than audio measurements.

 

[Arpiben]

Thanks. Please note that AP is using the total signal rms for THD+N ratio and fundamental for the others.
https://www.ap.com/technical-library/more-about-thdn-and-thd/

 

[atomicbob]

Thanks. Please note that AP is using the total signal rms for THD+N ratio and fundamental for the others.
https://www.ap.com/technical-library/more-about-thdn-and-thd/

The AP technical note you reference describes the difference between THD and THD+N measurements. While related in name, they are considerably different in how they are computed. Analyzers with which I am familiar calculate THD and THD+N the same way noted in the paper and also described in Fundamentals of Modern Audio Measurements to which I provided a link for further reading. Richard C. Cabot worked at Audio Precision for a period of time.