71 dB
Headphoneus Supremus
When I studied spatial hearing in university back in the 90's I was though Interaural Time Difference ITD to be
where π is the azimuth angle of sound, r is the radius of a rigid ball approximating head and c is the speed of sound. This formula is by Woodworth (1938). It is very intuitive, but is an accurate approximation only at high frequenicies. So, we should really write:
The intuitive nature of this formula made me believe it applies for all frequencies. It didn't occure to me the sound would travel differently "behind" the head at different frequencies.
Kuhn (1977) presented his formula for accurate approximation at low frequencies:
This means ITD at low frequencies is 17-47 % larger than at high frequencies in the spherical head model depending on azimuth angle π.
How about the transition band, where the ITD goes from Kuhn to Woodworth? The frequencies where the head is about the size of the wavelength. I wanted to create a formula that gives a good approximation for ITD as a function of frequency f. Such formula should have smooth transition from Kuhn to Woodworth. Let's first rewrite the two formula this way:
Now it is easier to see what is similar in the formulas and what is the part that needs to transition with frequency (bold). We can write:
where
This might look complex, but it is just a weighted sum of ITDLF and ITDHF so that the sum of the weights is exactly 1 at all frequencies:
In these weights fo is the threshold frequency that makes both weights 1/2 so that the ITD is the average of Woodworth and Kuhn. This threshold frequency makes it possible to fine-tune ITD(f). I have initially used the value fo = 630 Hz. Simplifying the formula for ITD gives:
The ITD curves look like this:
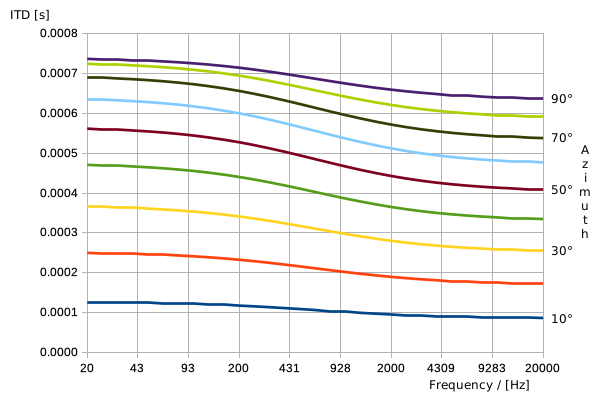
This is calculated using parameters fo = 630 Hz, r = 0.085 m and c = 345 m/s. So, this is for a small head and the ITD values are on the smaller side. Since Woolworths and Kuhn's formulas do not differentiate front and back angles, this combined formula doesn either, and only azimuth angles up to 90Β° at 10Β° steps are calculated.
How about the inverse function of this Woolworth-Kuhn formalu? How do we calculate the azimuth angle of sound from ITD? I have an approximative inverse function for Woolworth and for Kuhn's formula that inverse function is easy. These can be combined using the same strategy as with the ITD formula using the weighing parameters:
ITD = r/c * (sin π + π),
where π is the azimuth angle of sound, r is the radius of a rigid ball approximating head and c is the speed of sound. This formula is by Woodworth (1938). It is very intuitive, but is an accurate approximation only at high frequenicies. So, we should really write:
ITDHF = r/c * (sin π + π).
The intuitive nature of this formula made me believe it applies for all frequencies. It didn't occure to me the sound would travel differently "behind" the head at different frequencies.
Kuhn (1977) presented his formula for accurate approximation at low frequencies:
ITDLF = 3r/c * sin π.
This means ITD at low frequencies is 17-47 % larger than at high frequencies in the spherical head model depending on azimuth angle π.
How about the transition band, where the ITD goes from Kuhn to Woodworth? The frequencies where the head is about the size of the wavelength. I wanted to create a formula that gives a good approximation for ITD as a function of frequency f. Such formula should have smooth transition from Kuhn to Woodworth. Let's first rewrite the two formula this way:
ITDLF = r/c * (sin π + 2*sin π).
ITDHF = r/c * (sin π + π).
ITDHF = r/c * (sin π + π).
Now it is easier to see what is similar in the formulas and what is the part that needs to transition with frequency (bold). We can write:
ITD = r/c * (sin π + T(π, f )),
where
T(π, f ) = 2*sin π / (1+f/fo) + (f/fo)*π/(1+f/fo).
This might look complex, but it is just a weighted sum of ITDLF and ITDHF so that the sum of the weights is exactly 1 at all frequencies:
(1+f/fo) + (f/fo)/(1+f/fo) = (1+f/fo)/(1+f/fo) = 1.
In these weights fo is the threshold frequency that makes both weights 1/2 so that the ITD is the average of Woodworth and Kuhn. This threshold frequency makes it possible to fine-tune ITD(f). I have initially used the value fo = 630 Hz. Simplifying the formula for ITD gives:
ITD = r/c * (( 3*fo + f )*sin π + f *π ) / ( fo + f ).
The ITD curves look like this:
This is calculated using parameters fo = 630 Hz, r = 0.085 m and c = 345 m/s. So, this is for a small head and the ITD values are on the smaller side. Since Woolworths and Kuhn's formulas do not differentiate front and back angles, this combined formula doesn either, and only azimuth angles up to 90Β° at 10Β° steps are calculated.
How about the inverse function of this Woolworth-Kuhn formalu? How do we calculate the azimuth angle of sound from ITD? I have an approximative inverse function for Woolworth and for Kuhn's formula that inverse function is easy. These can be combined using the same strategy as with the ITD formula using the weighing parameters:
π β 180Β° * ((1- SQRT(1- 3*c*ITD / (2*r *(π+2)))) * (f/fo)/(1+f/fo) + ARCSIN(c * ITD / (3*r )) * (1+f/fo)).
Pretty awful equation, but spatial hearing is complex and even simple spherical approximations of head lead to nasty looking math...
